本文共 9083 字,大约阅读时间需要 30 分钟。
树中两个结点的最低公共祖先
问题(普通树)
求树中两个结点的最低公共祖先,此树不是二叉树,并且没有指向父节点的指针。
树的结点定义
private static class TreeNode { int val; List children = new LinkedList<>(); public TreeNode() { } public TreeNode(int val) { this.val = val; } @Override public String toString() { return val + ""; }} 题目解析
假设还是输入结点F和H .
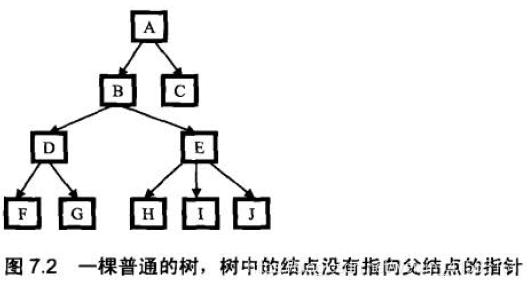
我们首先得到一条从根结点到树中某一结点的路径,这就要求在遍历的时候,有一个辅助内存来保存路径.比如我们用前序遍历的方法来得到从根结点到H 的路径的过程是这样的:
( 1 )遍历到A,把A 存放到路径中去,路径中只有一个结点A;
( 2 )遍历到B,把B 存到路径中去,此时路径为A->B;
( 3 )遍历到D,把D 存放到路径中去,此,时路径为A->B->D;
( 4 ) :遍历到F,把F 存放到路径中去,此时路径为A->B->D->F;
( 5) F 已经没有子结点了,因此这条路径不可能到这结点H. 把F 从路径中删除,变成A->B->D;
( 6 )遍历G. 和结点F 一样,这条路径也不能到达H. 边历完G 之后,路径仍然是A->B->D;
( 7 )由于D 的所有子结点都遍历过了,不可能到这结点H,因此D 不在从A 到H 的路径中,把D 从路径中删除,变成A->B;
( 8 )遥历E,把E 加入到路径中,此时路径变成A->B->E,
( 9 )遍历H,已经到达目标给点, A->B->E 就是从根结点开始到达H 必须经过的路径。
同样,我们也可以得到从根结点开始到达F 必须经过的路径是A->B功。接着,我们求出这两个路径的最后公共结点,也就是B. B这个结点也是F 和H 的最低公共祖先.
为了得到从根结点开始到输入的两个结点的两条路径,需要追历两次树,每边历一次的时间复杂度是O(n).得到的两条路径的长度在最差情况时是0(时,通常情况丁两条路径的长度是O(logn).
注意:可以在只遍历树一次就找到两个结点的路径,这部分留给读者自己去完成。
代码实现
public class Test1 { public static void main(String[] args) { test01(); System.out.println("=========="); test02(); System.out.println("=========="); test03(); } // 形状普通的树 // 1 // / \ // 2 3 // / \ // 4 5 // / \ / | \ // 6 7 8 9 10 public static void test01() { TreeNode n1 = new TreeNode(1); TreeNode n2 = new TreeNode(2); TreeNode n3 = new TreeNode(3); TreeNode n4 = new TreeNode(4); TreeNode n5 = new TreeNode(5); TreeNode n6 = new TreeNode(6); TreeNode n7 = new TreeNode(7); TreeNode n8 = new TreeNode(8); TreeNode n9 = new TreeNode(9); TreeNode n10 = new TreeNode(10); n1.children.add(n2); n1.children.add(n3); n2.children.add(n4); n4.children.add(n6); n4.children.add(n7); n3.children.add(n5); n5.children.add(n8); n5.children.add(n9); n5.children.add(n10); System.out.println(getLastCommonParent(n1, n9, n10)); } // 树退化成一个链表 // 1 // / // 2 // / // 3 // / // 4 // / // 5 private static void test02() { TreeNode n1 = new TreeNode(1); TreeNode n2 = new TreeNode(2); TreeNode n3 = new TreeNode(3); TreeNode n4 = new TreeNode(4); TreeNode n5 = new TreeNode(5); n1.children.add(n2); n2.children.add(n3); n3.children.add(n4); n4.children.add(n5); System.out.println(getLastCommonParent(n1, n4, n5)); } // 树退化成一个链表,一个结点不在树中 // 1 // / // 2 // / // 3 // / // 4 // / // 5 private static void test03() { TreeNode n1 = new TreeNode(1); TreeNode n2 = new TreeNode(2); TreeNode n3 = new TreeNode(3); TreeNode n4 = new TreeNode(4); TreeNode n5 = new TreeNode(5); TreeNode n6 = new TreeNode(6); n1.children.add(n2); n2.children.add(n3); n3.children.add(n4); n4.children.add(n5); System.out.println(getLastCommonParent(n1, n5, n6)); } /* * 获取两个节点的最低公共祖先 */ public static TreeNode getLastCommonParent(TreeNode root, TreeNode p1, TreeNode p2) { //path1和path2分别存储根节点到p1和p2的路径(不包括p1和p2) List path1 = new ArrayList<>(); List path2 = new ArrayList<>(); List tmpList = new ArrayList<>(); getNodePath(root, p1, tmpList, path1); getNodePath(root, p2, tmpList, path2); //如果路径不存在,返回空 if (path1.size() == 0 || path2.size() == 0) { return null; } return getLastCommonParent(path1, path2); } // 获取根节点到目标节点的路径 public static void getNodePath(TreeNode root, TreeNode target, List tmpList, List path) { //鲁棒性 if (root == null || root == target) { return; } tmpList.add(root); List children = root.children; for (TreeNode node : children) { if (node == target) { path.addAll(tmpList); break; } getNodePath(node, target, tmpList, path); } tmpList.remove(tmpList.size() - 1); } //将问题转化为求链表最后一个共同节点 private static TreeNode getLastCommonParent(List p1, List p2) { TreeNode tmpNode = null; for (int i = 0; i < p1.size(); i++) { if (p1.get(i) != p2.get(i)) { break; } tmpNode = p1.get(i); } return tmpNode; }} LeetCode
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
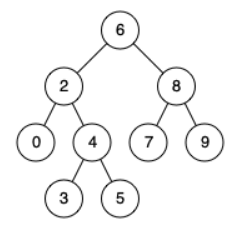
示例 1:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。
public static void main(String[] args) { TreeNode root = new TreeNode(6); TreeNode treeNode1 = new TreeNode(2); TreeNode treeNode2 = new TreeNode(8); TreeNode treeNode3 = new TreeNode(0); TreeNode treeNode4 = new TreeNode(4); TreeNode treeNode5 = new TreeNode(7); TreeNode treeNode6 = new TreeNode(9); TreeNode treeNode7 = new TreeNode(3); TreeNode treeNode8 = new TreeNode(5); root.left = treeNode1; root.right = treeNode2; treeNode1.left = treeNode3; treeNode1.right = treeNode4; treeNode2.left = treeNode5; treeNode2.right = treeNode6; treeNode4.left = treeNode7; treeNode4.right = treeNode8; System.out.println(LowestCommonAncestor(root,treeNode7,treeNode8).val);} public static TreeNode LowestCommonAncestor(TreeNode root,TreeNode p,TreeNode q){ if(p== null|| q==null|| root==null){ return null; } //遍历左子树 if(p.val < root.val && q.val < root.val){ return LowestCommonAncestor(root.left,p,q); } //遍历右子树 if(p.val > root.val && q.val > root.val){ return LowestCommonAncestor(root.right,p,q); } //如果左边大于等于,右边小于等于,直接返回root if(p.val <= root.val && q.val >= root.val){ return root; } return root;} 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
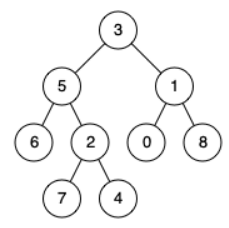
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉树中。
思路:
从上往下遍历,判断根结点是否匹配两个节点之一,
如果是,则根结点就是最低祖先,否则往下递归遍历左右子树
如果两个节点在不同的左右子树,则根结点是最低祖先
如果两个节点都出现在左子树,则左节点为最低祖先
如果两个节点都出现在右子树,则右节点为最低祖先
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode(int x) { val = x; } * } */class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if(root == null || root == q || root == p){ return root; } TreeNode left = lowestCommonAncestor(root.left,p,q); TreeNode right = lowestCommonAncestor(root.right,p,q); if(left != null && right != null){ return root; } return left == null ? right : left; }} public class Test2 { /** * 思路(非递归): * 1、找到root->p的路径 * 2、找到root->q的路径 * 3、两条路径求最后一个相交节点 */ public static TreeNode lowestCommonAncestorII(TreeNode root, TreeNode p, TreeNode q) { if (root == null || p == root || q == root) { return root; } List pPath = findPath(root, p); List qPath = findPath(root, q); TreeNode common = null; for (int i=0, j=0; i findPath(TreeNode root, TreeNode node) { List path = new ArrayList<>(); dfs(root, node, new ArrayList<>(), path); return path; } private static void dfs(TreeNode root, TreeNode node, List tmp, List path) { if (root == null) { return; } tmp.add(root); if (root == node) { path.addAll(new ArrayList<>(tmp)); } dfs(root.left, node, tmp, path); dfs(root.right, node, tmp, path); tmp.remove(tmp.size()-1); } public static void main(String[] args) { TreeNode root = new TreeNode(1); TreeNode right = new TreeNode(2); root.right = right; TreeNode left = new TreeNode(3); root.left = left; System.out.println(lowestCommonAncestorII(root, left, right).val); }} (未完待续)
给你一个有根节点的二叉树,找到它最深的叶节点的最近公共祖先。
回想一下:
叶节点 是二叉树中没有子节点的节点
树的根节点的 深度 为 0,如果某一节点的深度为 d,那它的子节点的深度就是 d+1
如果我们假定 A 是一组节点 S 的 最近公共祖先,<font color="#c7254e" face="Menlo, Monaco, Consolas, Courier New, monospace">S</font> 中的每个节点都在以 A 为根节点的子树中,且 A 的深度达到此条件下可能的最大值。
示例 1:
输入:root = [1,2,3]
输出:[1,2,3]
示例 2:
输入:root = [1,2,3,4]
输出:[4]
示例 3:
输入:root = [1,2,3,4,5]
输出:[2,4,5]
提示:
给你的树中将有 1 到 1000 个节点。
树中每个节点的值都在 1 到 1000 之间。

转载地址:http://tnzu.baihongyu.com/